Estimating square roots using the Newton-Raphson method
As early as 1000BC, Babylon had an algorithm in place to calculate the square root of any positive integer. We’ll look closer at this method and you can find its implementation in Python at the bottom.
Say you were to calculate the square root of 2. We can take a guess and pick a number that is half of 2 – so we pick 1. We’ll call this guess \(x_0\) and we will assign the name \(a\) to 2.
\(x_0^{2} = 1^2 = 1\), which is less than \(a\).
If we divide \(a\) by \(x_0\) we get \(\frac{2}{1} = 2\), and \(2^2 = 4\) which is greater than \(a\). We’ll take the arithmetic mean of \(x_0\) and \(\frac{2}{1}\), because our final solution would have to be somewhere in the middle. This mean will be our next “guess” \(x_1\). So, we have
\(x_1 = \frac{1}{2}(x_0 + \frac{2}{1})\)\(x_1 = \frac{1}{2}(1 + 2)\)
\(x_1 = \frac{3}{2} = 1.5\)
1.5 is really close to \(\sqrt{2}\), which is approximately 1.41. If we want, we can repeat the above calculation for our next guess \(x_2\):
\(x_2 = \frac{1}{2}(x_1 + \frac{2}{1.5})\)\(x_2 = \frac{1}{2}(1.5 + \frac{4}{3})\)
\(x_2 \approx 1.41\)
We therefore obtain the recursive formula
\(x_{n+1}= \frac{1}{2}(x_n + \frac{a}{x_n})\) for any positive integer \(a\).
Newton and Raphson used calculus to derive a similar method for any real function \(f(x)\). Assume there exists a root \(r\) of function \(f(x)\) such that \(f(r) = 0\) (i.e. zero of a function). If we pick a value \(x_0\) that is close to \(r\) and draw a tangent to the graph of \(f(x)\) at that point, then the point where the tangent cuts the x-axis will give us the next value \(x_1\) that is even closer to \(r\). We can keep repeating this procedure and we obtain the general formula:
\(x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}\)
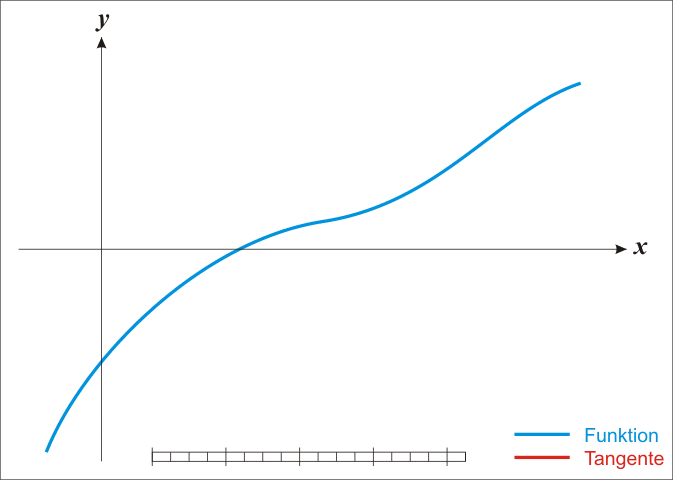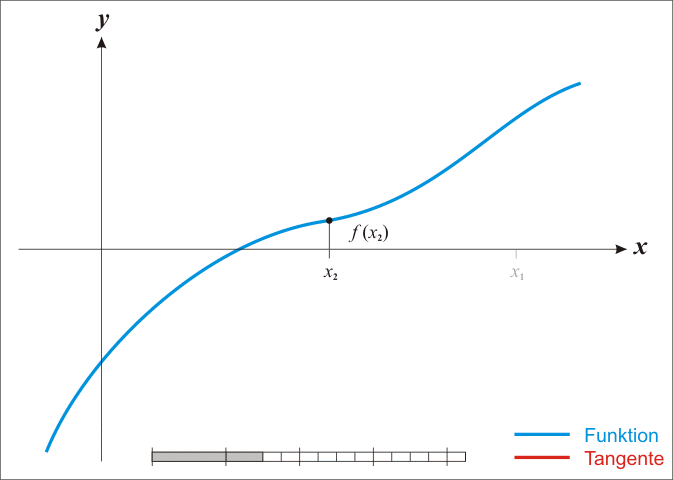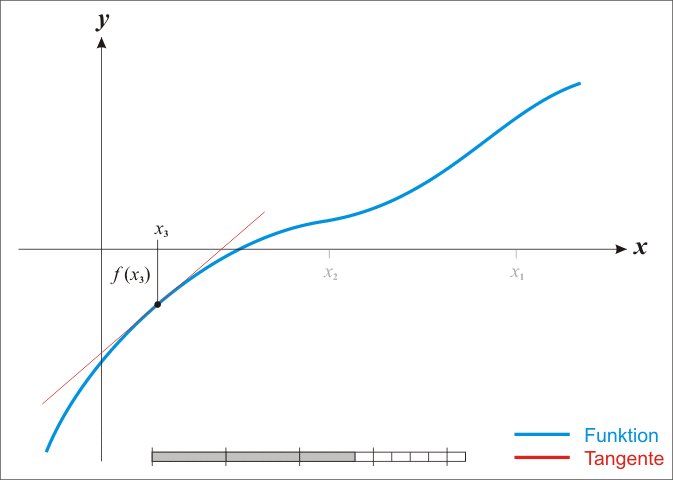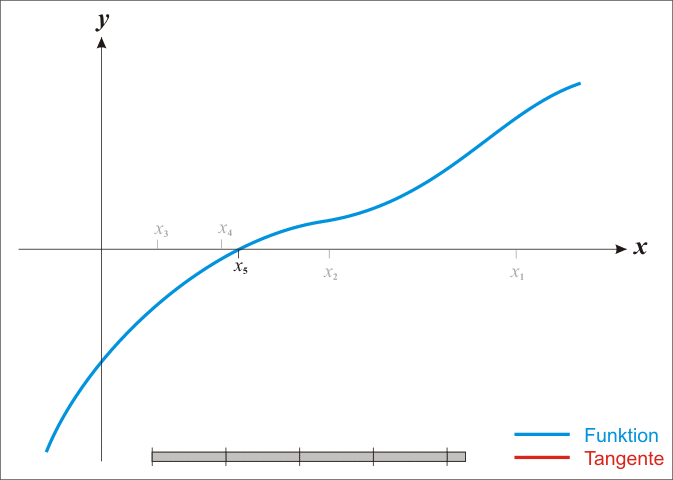
By Ralf Pfeifer – de:Image:NewtonIteration Ani.gif, CC BY-SA 3.0, Link
The square root estimation method can be implemented in Python as:
def newton_sqrt(n, guess, convergence=2):
"""Uses the Newton-Raphson method of finding the square root of n.
guess: initial estimate.
convergence: number of decimal places at which the approximation is
considered accurate.
"""
if (n == 1):
return n
approximation = (guess + (n/guess))/2
rapprox = round(approximation, convergence)
rguess = round(guess, convergence)
if (rapprox == rguess):
return approximation
else:
return newton_sqrt(n, approximation, convergence)
The recursive function takes \(n\) as the number we would like to find the square root of and an initial guess \(x_0\). Convergence indicates the number of decimal digits that we will use to compare, as the values will be approximations. It is 2 by default.
If \(n\) is 1 then we just return the same value, since the square root of 1 is 1. Otherwise, we apply the estimation formula and round the approximate answer to the value specified by convergence. We apply the same rounding to the guess and check if it is the same as the approximate answer. If so, we return it as we are satisfied with the accuracy. If not, we call the function again with new guesses until they converge to the square root.
It’s worth noting that this algorithm performs faster the closer the initial guess is to the square root. Additionally, my profiling suggests that a lower convergence will also make the function run faster, with the round() function working slower when rounding to more decimals.